STAT 453

Lecture 10

Regularization and Generalization

Today’s Topics:

0. From last lecture: Kaggle Cats & Dogs + DataLoader

Kaggle is a platform for hosting datasets and machine learning competitions. Organizations (companies, research groups, or nonprofits) upload datasets and define an evaluation metric. Participants train models and submit predictions; the best-performing models appear at the top of the leaderboard and may receive prizes.

Reference notebook (VGG16 on Cats vs. Dogs):

Why PyTorch Dataset and DataLoader are needed

Real-world datasets (especially images) are often too large to load into memory at once. PyTorch separates data handling into two components:

This design enables efficient, scalable training by streaming data batch-by-batch instead of loading the full dataset at once. Custom DataLoader example notebook:

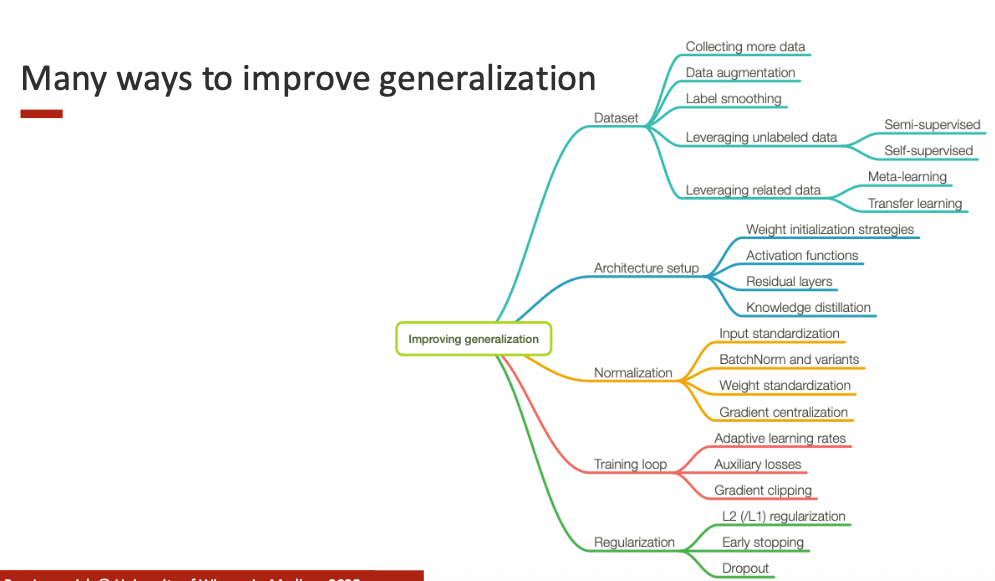
1. Improving Generalization

Generalization refers to how well a trained model performs on unseen data.
A model that generalizes well captures the true underlying patterns in the dataset instead of memorizing noise from the training set.

Achieving high training accuracy is not enough — the goal is to ensure that the model performs well on new data.
Overfitting occurs when a model is too closely tailored to the training set, leading to poor test performance.

Key strategies to improve generalization:

Figure 1. Strategies for improving model generalization.

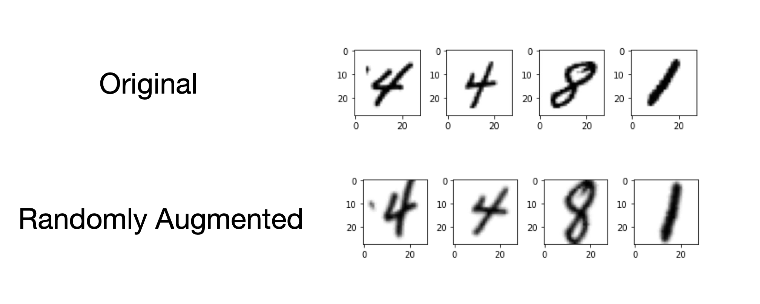
2. Data Augmentation

Data augmentation increases dataset size by generating label-preserving transformations — improving robustness and reducing overfitting.
Useful when labeled data is scarce or costly (e.g., medical imaging).

Common augmentations:

These simulate real-world variations and encourage invariant feature learning.

\mathcal{D}_{\mathrm{aug}} = \{ (h(x_i), y_i) \mid (x_i, y_i)\in\mathcal{D} \}
Figure 2. Original vs. augmented data.

3. Early Stopping

Reducing Model Capacity

Another way to improve generalization is to reduce the effective capacity of the model.

Common approaches include:

In modern deep learning, it is common to start with a large pretrained model and control capacity through regularization and selective fine-tuning rather than training small models from scratch.

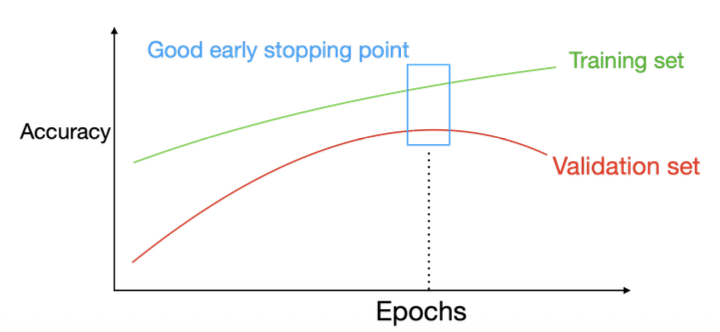
Early Stopping

Early stopping halts training when validation performance stops improving — preventing overfitting.

Procedure

  1. Split data into training/validation/test.
  2. Track validation performance.
  3. Stop training when validation loss stops decreasing.
Figure 3. Early stopping accuracy curve.
Figure 4. Early stopping loss curve.

4. L1 and L2 Regularization

Regularization penalizes large weights, encouraging simpler models and preventing overfitting.L1 regularization corresponds to LASSO, while L2 regularization corresponds to Ridge regression

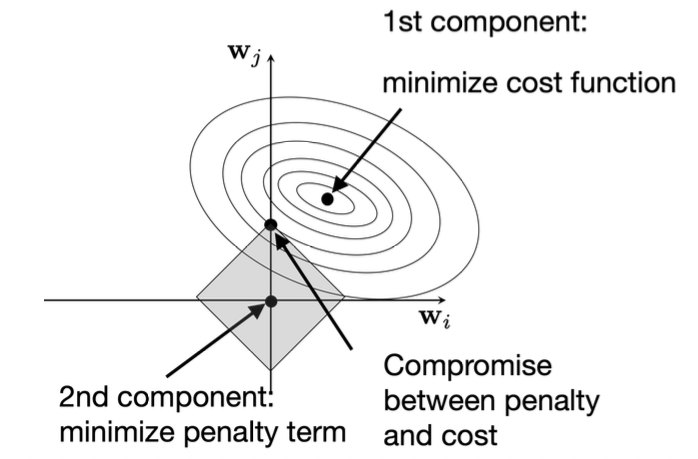
4.1 L1 Regularization (Lasso)

\(\mathcal{L}_{L1} = \frac{1}{n}\sum_{i=1}^{n} L(y^{[i]}, \hat{y}^{[i]}) + \frac{\lambda}{n}\sum_{j} |w_j|\)

-L1 Regularization (Lasso) adds the sum of the absolute values of all weights as a penalty term to the loss function, helping to control model complexity.

-It drives many weights to zero, producing a sparse solution and enabling automatic feature selection.

-Geometrically, the circular contours represent the cost function, while the diamond shape represents the L1 constraint boundary. The model seeks a balance between minimizing the loss and satisfying the constraint.

-Because the diamond has sharp corners that align with the coordinate axes, the optimal point often lies on an axis, causing some weights to become exactly zero.

-This regularization prevents overfitting and makes the resulting model simpler and more interpretable.

Figure 5. L1 regularization promotes sparsity.

4.2 L2 Regularization (Ridge)

\[\mathcal{L}_{L2} = \frac{1}{n}\sum_{i=1}^{n} L(y^{[i]}, \hat{y}^{[i]}) + \frac{\lambda}{n}\sum_{j} w_j^2\]

w_{i,j} := w_{i,j} - \eta!\left(\frac{\partial L}{\partial w_{i,j}} + \frac{2\lambda}{n}w_{i,j}\right) </d-math>

-L2 Regularization (Ridge) adds the sum of squared weights as a penalty term to the loss function, discouraging large coefficients.

-Unlike L1, it does not force weights to zero, but instead smooths them toward smaller values, distributing the influence more evenly among features.

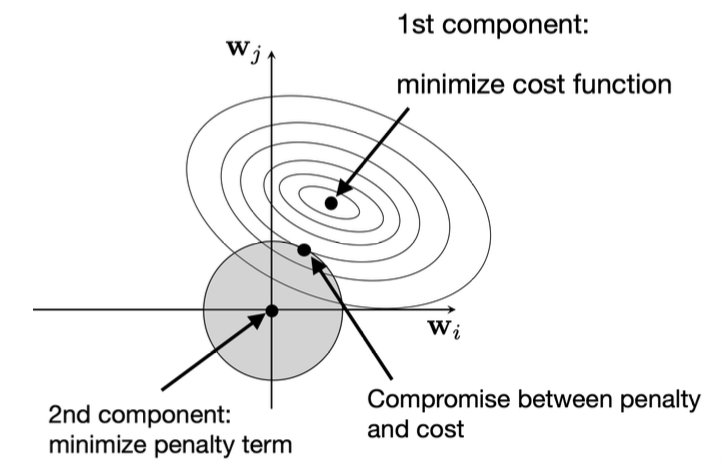
-Geometrically, the circular contour lines represent the cost function, while the gray circle represents the L2 constraint.

-The optimal point lies where the cost contour just touches the constraint circle, balancing the trade-off between minimizing the cost and the penalty term.

-Because the circle has no sharp corners, all weights are shrunk but rarely become zero, which means L2 encourages weight smoothing rather than sparsity.

Figure 6. L2 regularization smooths weight distribution.

5. Dropout

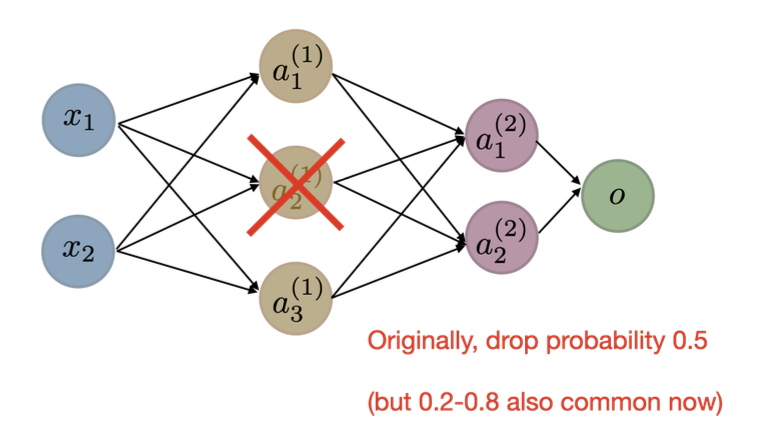
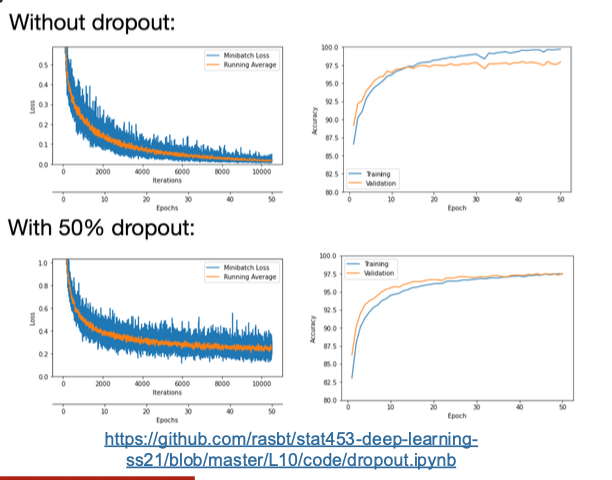
Dropout randomly removes a fraction of neurons during training — forcing the network to learn redundant, distributed representations.

Why it works

\tilde{h}_i = z_i h_i,\quad z_i = \begin{cases} 0 & \text{with probability } p \\ 1 & \text{with probability } 1-p \end{cases}
Figure 7. Dropout training process.
Figure 8. Dropout improves validation accuracy.

Summary

Regularization and generalization methods — like data augmentation, early stopping, L2, and dropout — are essential to ensure models learn meaningful patterns, not noise.
They enable robust generalization and stable performance on unseen data.

© 2025 University of Wisconsin — STAT 453 Lecture Notes