STAT 453

Lecture 21: GPT Architectures

From RNNs to Transformers to GPT - Understanding the evolution of modern language models

Today’s Topics:

Part 1: From RNN to Self-Attention & The Transformer

(Ref: Slides 1–10, 15–16)

1. The Limitations of RNNs

(Ref: Slides 2–3)

Recurrent Neural Networks (RNNs) were the dominant architecture for sequence modeling before the Transformer era. RNNs process sequences sequentially, maintaining a hidden state $h^{\langle t \rangle}$ that gets updated at each time step:

h^{\langle t \rangle} = f(W_{hh} h^{\langle t-1 \rangle} + W_{hx} x^{\langle t \rangle}) y^{\langle t \rangle} = g(W_{yh} h^{\langle t \rangle})

While this recurrent structure allows the model to process sequences of arbitrary length, it introduces several critical problems:

  1. Sequential Processing Bottleneck: Each token must be processed one at a time, meaning computation cannot be parallelized across the sequence. This makes training extremely slow for long sequences.

  2. Long-Range Dependency Problem: Information from early tokens must be passed through many intermediate hidden states to reach later positions. Despite improvements like LSTMs and GRUs, gradients still tend to vanish or explode over long sequences, making it difficult to capture dependencies between distant tokens.

  3. Fixed-Capacity Hidden State: The entire sequence history must be compressed into a single fixed-dimensional vector $h^{\langle t \rangle}$, creating an information bottleneck.

Key Insight: We need an architecture that:

This motivates the Transformer architecture.

2. The Transformer Solution

(Ref: Slides 4–5)

The Transformer, introduced by Vaswani et al. (2017) in “Attention Is All You Need,” replaces recurrence with attention mechanisms. Instead of sequentially processing tokens, the Transformer computes interactions between all pairs of positions in parallel using self-attention.

Key advantages:

The Transformer consists of:

3. Self-Attention: The Basic (Non-Learnable) Form

(Ref: Slide 6)

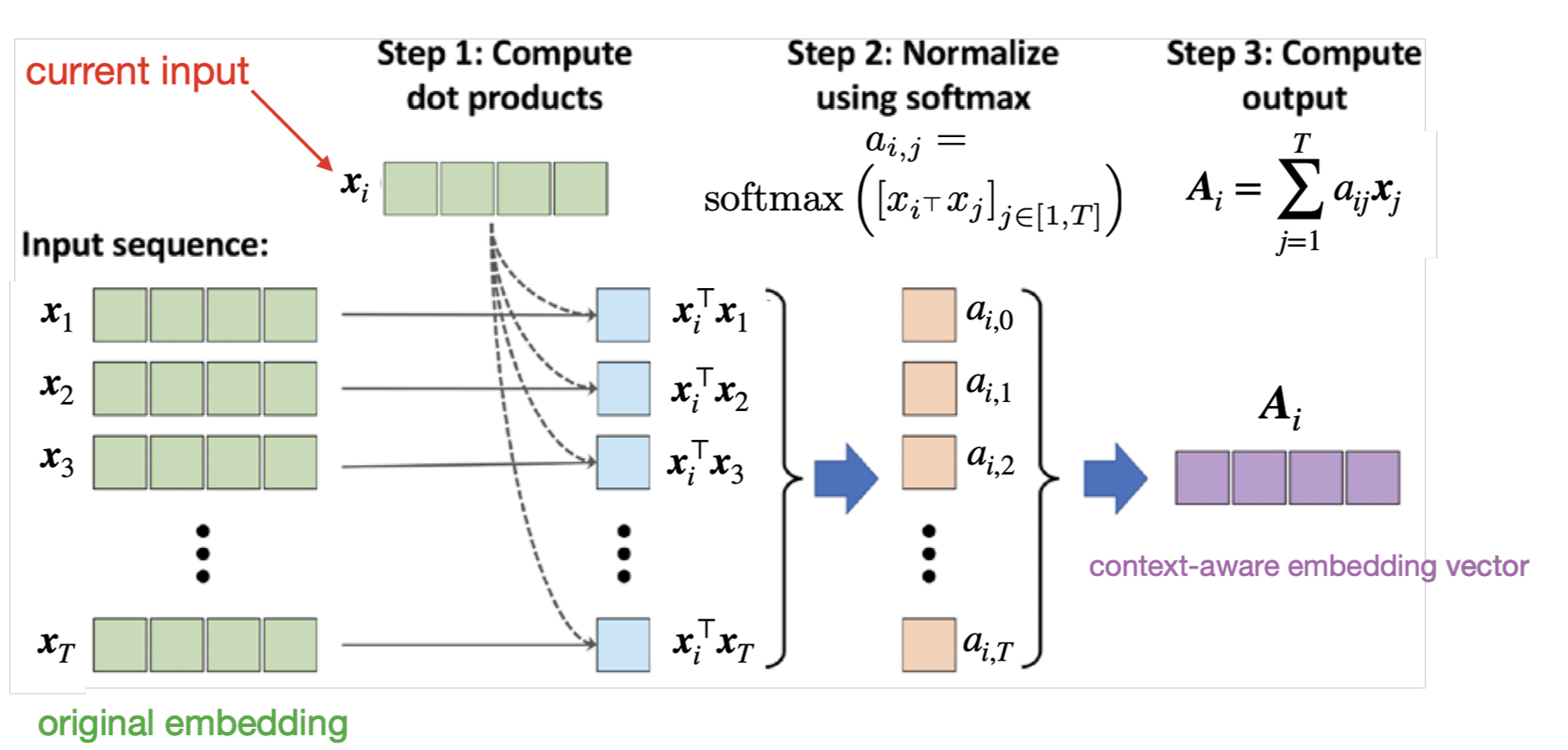
Before introducing the learnable self-attention used in Transformers, let’s understand the simplest form of self-attention to grasp the core concept.

Given a sequence of token embeddings:

X = [x_1, x_2, \ldots, x_T] \in \mathbb{R}^{T \times d}

where $T$ is the sequence length and $d$ is the embedding dimension.

Step 1: Compute similarity scores between the current token $x_i$ and all tokens $x_j$:

\text{score}_{ij} = x_i^{\top} x_j

This is simply the dot product between embeddings, measuring their similarity.

Step 2: Normalize scores using softmax to get attention weights:

a_{i,j} = \text{softmax}\left([x_i^{\top} x_j]_{j \in [1,T]}\right) = \frac{\exp(x_i^{\top} x_j)}{\sum_{j'=1}^{T} \exp(x_i^{\top} x_{j'})}

These weights $a_{i,j}$ sum to 1 across all $j$ for each position $i$.

Step 3: Compute context-aware representation as a weighted sum:

A_i = \sum_{j=1}^{T} a_{ij} \cdot x_j

The output $A_i$ is called a context-aware embedding vector because it incorporates information from all positions in the sequence, weighted by their relevance to position $i$.

Problem: This basic form has no learnable parameters! The model cannot learn what types of relationships to capture. The similarity is purely based on the raw embeddings.

4. Learnable Self-Attention: Query, Key, Value

(Ref: Slides 7–8)

To make self-attention learnable, we introduce three trainable weight matrices that transform the input embeddings:

\text{query} = W^q x_i, \quad \text{key} = W^k x_i, \quad \text{value} = W^v x_i

where:

For the entire sequence, we compute:

Q = X W^q, \quad K = X W^k, \quad V = X W^v

Intuition:

Scaled Dot-Product Attention

The attention mechanism computes:

Step 1: Compute attention scores (compatibility between queries and keys):

\text{score}_{ij} = \frac{q_i^{\top} k_j}{\sqrt{d_k}}

The scaling by $\sqrt{d_k}$ prevents the dot products from becoming too large (which would cause softmax to saturate).

Step 2: Apply softmax to get attention weights:

a_{ij} = \frac{\exp(\text{score}_{ij})}{\sum_{j'=1}^{T} \exp(\text{score}_{ij'})}

This is a form of similarity or compatibility measure (multiplicative attention). The softmax ensures weights are normalized and can be interpreted as probabilities.

Step 3: Weighted aggregation of values:

h_i = \sum_{j=1}^{T} a_{ij} \cdot v_j

Or in matrix form for the entire sequence:

\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^{\top}}{\sqrt{d_k}}\right) V

Key Insight: For each query position $i$, the model learns which key-value pairs to attend to. The attention weights $a_{ij}$ tell us how much position $i$ should focus on position $j$.

5. Multi-Head Attention

(Ref: Slide 9)

Instead of performing attention once, Transformers use multiple attention heads operating in parallel. Each head can learn to capture different types of relationships:

\text{head}_h = \text{Attention}(Q W_h^Q, K W_h^K, V W_h^V)

The outputs of all heads are concatenated and linearly transformed:

\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_H) W^O

where $W^O$ is an output projection matrix.

Benefits:

Example from Slide 9: In the sentence “It is in this spirit that a majority of American governments have passed new laws since 2009 making the registration or voting process more difficult”, different attention heads capture:

6. The Complete Transformer Architecture

(Ref: Slides 10, 15–16)

The original Transformer consists of two main components:

A. Encoder Stack (Left side)

The encoder processes the entire input sequence using:

  1. Input Embedding: Converts tokens to dense vectors
  2. Positional Encoding: Adds position information (since attention is permutation-invariant) PE*{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d}}\right) PE*{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d}}\right)
  3. $N_x$ Encoder Layers, each containing:
    • Multi-Head Self-Attention: Full bidirectional attention (every position can attend to every other position)
    • Add & Norm: Residual connection + Layer Normalization
    • Feed-Forward Network: Position-wise FFN applied independently to each position \text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2
    • Add & Norm: Another residual connection + Layer Normalization

Key feature: The encoder uses bidirectional (full) self-attention - each token can see all other tokens in both directions. This is optimal for understanding the input context.

B. Decoder Stack (Right side)

The decoder generates the output sequence autoregressively using:

  1. Output Embedding + Positional Encoding (shifted right during training)
  2. $N_x$ Decoder Layers, each containing:
    • Masked Multi-Head Self-Attention: Causal attention that prevents positions from attending to future positions
      • Uses a mask to set attention scores for future positions to $-\infty$ before softmax
      • Ensures autoregressive property: position $t$ can only attend to positions $\leq t$
    • Add & Norm
    • Multi-Head Cross-Attention: Attends to the encoder’s output
      • Queries come from the decoder
      • Keys and Values come from the encoder output
      • Allows decoder to focus on relevant parts of the input
    • Add & Norm
    • Feed-Forward Network
    • Add & Norm
  3. Linear + Softmax: Projects to vocabulary size and produces token probabilities

Key features:

Design Principles

The Transformer architecture embodies several key principles:

  1. Parallelization: Unlike RNNs, all positions in a sequence can be processed simultaneously
  2. Residual Connections: Help with gradient flow in deep networks
  3. Layer Normalization: Stabilizes training
  4. Position-wise FFN: Adds non-linearity and increases model capacity
  5. Positional Encodings: Inject order information into the otherwise permutation-invariant attention

Original Use Case: The Transformer was designed for machine translation, where:

This encoder-decoder structure with cross-attention is ideal for tasks where you have a complete input sequence and need to generate a related output sequence.

Part 2: GPT Architecture & Probabilistic Model

(Ref: Slides 11–14, 17–21)

1. Architecture Simplification: From Transformer to GPT

GPT (Generative Pre-trained Transformer) represents a significant architectural shift from the original Transformer model.

A. The “Decoder-Only” Architecture

The original Transformer consisted of two main blocks:

  1. Encoder: Processes the input sequence (bidirectional attention).
  2. Decoder: Generates the output sequence (masked unidirectional attention) + Cross-attention to the encoder.

GPT simplifies this by removing the Encoder entirely.

B. Masked Self-Attention (Causal Masking)

This is the critical component that defines GPT’s behavior.

2. Probabilistic Modeling: Next-Token Prediction

A. The Formula (Chain Rule of Probability)

Given a sequence of tokens $U = {u_1, u_2, …, u_n}$, the joint probability of the entire sequence $P(U)$ is factored using the chain rule:

$P(U) = \prod_{i=1}^{n} P(u_i \mid u_{1}, \dots, u_{i-1})$

B. Training Objective

We define the loss function (typically Cross-Entropy) as:

$\mathcal{L}(\theta) = - \sum_{i} \log P(u_i \mid u_{i-k}, \dots, u_{i-1}; \theta) $

C. Directed Probabilistic Graphical Model

GPT can be viewed as a directed PGM:

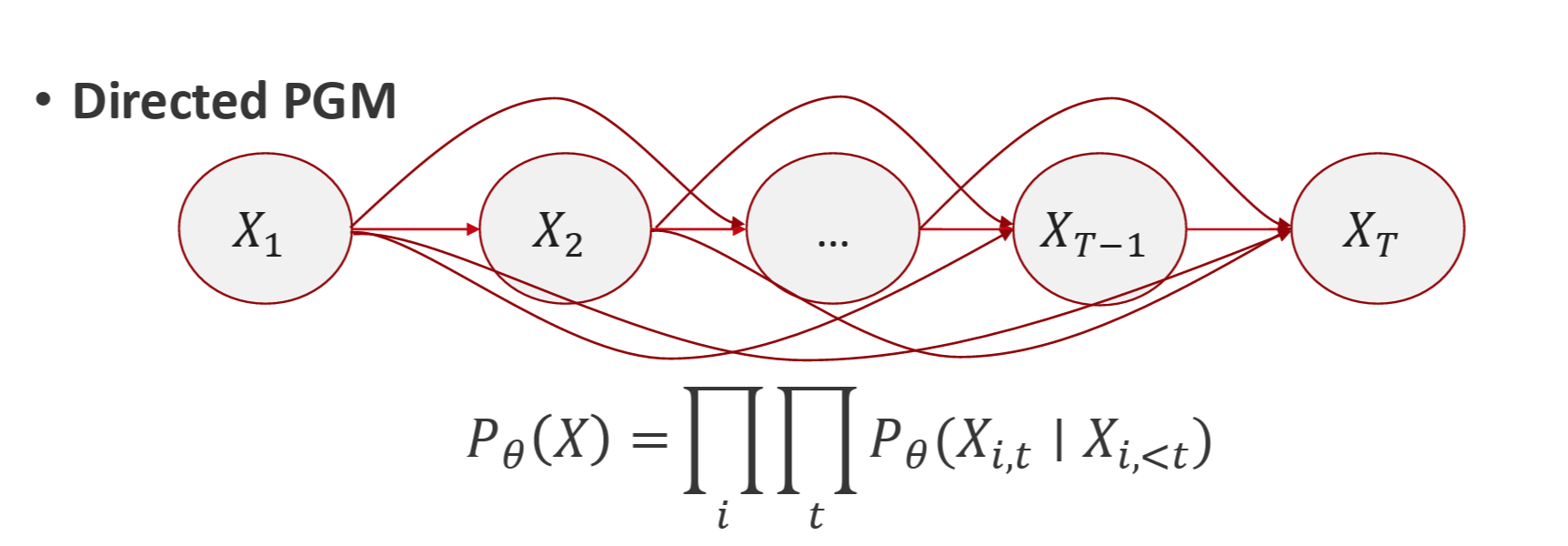
$P_{\theta}(X) = \prod_i \prod_t P_{\theta} (X_{i,t} \mid X_{i,<t})$

when we transform this probability into log-likelihood form, the probabilistic objective becomes maximizing :

$\max_{\theta} \sum_{i} \sum_{t} \log P_{\theta} (X_{i,t} \mid X_{i,<t})$

which corresponds to MLE objective.

Model structure:

3. GPT vs. Traditional Seq2Seq (Translation)

How does GPT differ from traditional Sequence-to-Sequence models (like the original Transformer or LSTM-based translation models)?

A. Traditional Seq2Seq (Encoder-Decoder)

Used typically for translation ($English \rightarrow French$).

B. GPT (Autoregressive Language Model)

GPT does not have a separate “source” encoding stage. It treats Translation as Conditioned Generation.

Summary Table

Feature Traditional Seq2Seq (e.g., T5) GPT (Decoder-Only)
Architecture Encoder-Decoder Decoder-Only
Attention Bidirectional (Enc) & Causal (Dec) Causal (Masked) Only
Objective Masked Language Modeling / Translation Next-Token Prediction
Task Approach Task-specific fine-tuning structure Few-shot prompting (Input concatenation)

Part 3: The Evolution of the GPT Series (GPT-1 to GPT-4)

(Ref: Slides 22–26, 36)

1. From our “GPT-0” to GPT-1

(Ref: Slide 23)

Moving from a simple character-level GPT to GPT-1 involves several key improvements:

Architecture Changes:

Scale (117M parameters):

Training:

Inference:

2. From GPT-1 to GPT-2

(Ref: Slide 24)

GPT-2 demonstrated that language models could be “unsupervised multitask learners.”

Architecture:

Scale options, with largest model at 1.5B parameters:

Training:

Note: You can reproduce GPT-2 yourself using Andrej Karpathy’s nanoGPT (takes 4 days on an 8xA100 machine)

3. From GPT-2 to GPT-3

(Ref: Slide 25)

GPT-3 demonstrated that with sufficient scale, language models become “few-shot learners.”

Architecture:

Massive scale increase to 175B parameters:

Training:

Key Innovation: Few-shot and zero-shot learning capabilities emerge at scale

4. From GPT-3 to GPT-4

(Ref: Slide 26)

GPT-4 represents a leap in capabilities with architectural innovations and alignment improvements.

Architecture:

Scale:

Training:

5. Comparison Table: GPT-1 to GPT-4

Model Number of parameters Training data Context window Tokenizer Architecture New capabilities
GPT-1 117M 5GB 512 BPE Layers: 12
Heads: 12
Emb dim: 768
Vocab: 40K		 Transfer learning
GPT-2 1.5B 40GB 1024 BPE Layers: 48
Heads: 25
Emb dim: 1600
Vocab: 50K		 Zero-shot learning
GPT-3 175B ~570GB 2048 BPE Layers: 96
Heads: 96
Emb dim: 12288
Vocab: >50K		 Few-shot learning
GPT-4 Likely >1T ~50TB 128K Text + image patches MoE (likely)
• Larger scale (depth/width)		 • RLHF
• Multimodal
• Long-context reasoning

Key Trends:

Part 4: Mixture of Experts (MoE) & Final Summary

(Ref: Slides 27–35)

1. Mixture of Experts (MoE): Architecture

As models scale (e.g., GPT-4), Mixture of Experts (MoE) decouples total model capacity from computational cost, allowing for massive parameter counts without slowing down inference.

A. The Core Idea

Mixture of Experts Architecture. A router network selects which expert(s) to activate for each token.

B. Dense vs. Sparse Models

Dense Model:

Sparse Model (MoE):

C. MoE in Transformer Decoder

The FFNN layer in each Transformer block is replaced with multiple expert FFNNs:

Dense Decoder:

Layer Norm → Masked Self-Attention → Add & Norm →
Layer Norm → [FFNN] → Add & Norm

Sparse Decoder (MoE):

Layer Norm → Masked Self-Attention → Add & Norm →
Layer Norm → [Router → Select Experts → FFNN₁, FFNN₂, ..., FFNNₙ] → Add & Norm

The router computes:

\text{MoE}(x) = \sum_{i=1}^{N} g_i(x) \cdot \text{Expert}_i(x)

where $g_i(x)$ is the gating weight for expert $i$.

2. Probabilistic View of MoE

MoE acts as a probabilistic ensemble where the contribution of each expert is dynamic. The output probability $P(Y \mid X)$ is:

P(Y | X) = \sum_{m} g_m(X) \cdot P_m(Y | X)

where:

Constraints:

\sum_{m} g_m(X) = 1, \quad g_m(X) \geq 0 \quad \forall m, X

This formulation unifies several ensemble approaches:

Comparison with Other Ensemble Methods:

Method Gating Function $g_m(X)$ Description
Bagging $g_m(X) = \frac{1}{M}$ Constant, uniform weighting across all experts
Boosting $g_m(X) = \alpha_m$ Constant but expert-specific weights
MoE $g_m(X) = \text{Router}(X)$ Learned function of the input - adapts per example

Key Insight: In MoE, the gating function $g_m(X)$ is input-dependent. The model learns to route specific types of inputs to specific experts, enabling specialization.

3. Error Analysis: The Role of Diversity

The goal of MoE is to minimize the Ensemble Error rather than the individual Average Expert Error.

A. Error Definitions

Define:

Compare:

B. Analysis for Linear Models

For linear experts $f_m$, we can decompose the errors:

Error vs. Diversity Trade-off. As expert diversity increases (more unique training data), ensemble error decreases while average expert error increases. The disagreement between experts (dashed line) shows why diverse experts help.

Key Observations:

  1. Ensemble error decreases with diversity (solid line, lower)
  2. Average expert error increases with diversity (solid line, upper)
  3. Disagreement between experts (dashed line) increases with diversity

Intuition: Expert errors are wrong in individualized ways and cancel out through consensus.

\text{Ensemble Error} < \text{Average Expert Error} \quad \text{when experts are diverse}

→ Slight “overfitting” of experts helps!

Experts that specialize (even overfit) to different data subsets create diversity, which reduces ensemble error even if individual expert errors are higher.

4. Implications for LLMs

A. Training Implications

From the error analysis, we learn:

Common training challenge: Experts can collapse to similar solutions, reducing diversity.

Solutions include:

B. Serving Implications

MoE Serving Architecture. Shows the router network selecting experts and the gating mechanism for combining expert outputs.

Benefits:

Challenges:

5. Summary: Transformer vs. GPT

While GPT originates from the Transformer architecture, it evolved specifically for generative tasks.

Component Original Transformer (Vaswani et al., 2017) GPT (Generative Pre-Trained Transformer)
Architecture Encoder-Decoder (Full sequence transduction) Decoder-only (Unconditional generation)
Attention Full self-attention (Bidirectional in encoder) Masked (Causal) self-attention
Positional Encoding Sinusoidal (Fixed function) Learned positional embeddings (GPT-1+)
Output Task-specific (e.g., translation) Next-token prediction (Softmax)
Training Objective Flexible / Supervised (task-specific) Language Modeling (Autoregressive)
Inference Processes full input, generates full output Greedy / Sampling (Token-by-token)
Use Case Machine translation, seq2seq tasks Text generation, few-shot learning

6. Summary: From GPT-1 to GPT-4

The evolution of GPT models shows consistent trends:

Architectural Evolution:

Data Evolution:

Capability Evolution:

Architectural Innovations:

Conclusion

This lecture traced the evolution from RNNs through Transformers to modern GPT architectures:

  1. RNNs had fundamental limitations in parallelization and long-range dependencies
  2. Transformers solved these with self-attention and parallel processing
  3. GPT simplified the Transformer to a decoder-only architecture focused on language modeling
  4. Scaling from GPT-1 to GPT-4 showed that increased capacity, data, and training enable emergent capabilities
  5. Mixture of Experts enables continued scaling by decoupling model capacity from computational cost

The key insights are:

References

  1. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L. and Polosukhin, I., 2017. Attention Is All You Need. NeurIPS 2017.

  2. Radford, A., Narasimhan, K., Salimans, T. and Sutskever, I., 2018. Improving Language Understanding by Generative Pre-Training. OpenAI.

  3. Radford, A., Wu, J., Child, R., Luan, D., Amodei, D. and Sutskever, I., 2019. Language Models are Unsupervised Multitask Learners. OpenAI.

  4. Brown, T., Mann, B., Ryder, N., et al., 2020. Language Models are Few-Shot Learners. NeurIPS 2020.

  5. OpenAI, 2023. GPT-4 Technical Report.

  6. Jacobs, R.A., Jordan, M.I., Nowlan, S.J. and Hinton, G.E., 1991. Adaptive Mixtures of Local Experts. Neural Computation.

  7. Jordan, M.I. and Jacobs, R.A., 1994. Hierarchical Mixtures of Experts and the EM Algorithm. Neural Computation.

  8. Shazeer, N., et al., 2017. Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer. ICLR 2017.

  9. Sollich, P. and Krogh, A., 1995. Learning with Ensembles: How Overfitting Can Be Useful. NeurIPS 1995.

  10. Yang, L., et al., 2023. A Survey on Transformers. arXiv preprint.

  11. Grootendorst, M., A Visual Guide to Mixture of Experts. Blog post.

  12. Xie, S., et al., 2022. On the Role of the Action Space in Robot Manipulation Learning. arXiv preprint.